Total functions and beyond
On continuous benefits and extending spectra
Our last Apropos was with Sean Corfield. Check it out. Our next episode is with Bobbi on Tuesday March 25. Please watch us live so you can ask questions.
Have you seen Grokking Simplicity, my book for beginners to functional programming? Please check it out or recommend it to a friend. You can also get it from Manning. Use coupon code TSSIMPLICITY for 50% off.
Total functions and beyond
What is a total function?
A total function returns a valid value for all valid argument values. The opposite is a partial function. These terms come from mathematics.
A classic example of a partial function is division. Let’s look at it from a programming perspective:
function divide(a: number, b: number): number;This says that for any two numbers a and b, divide() will return a number. But this is a lie: If b is zero, there is no answer. It’s undefined in mathematical division.
In JavaScript (and TypeScript), division by zero is possible and well-defined:
1/0 => Infinity
-1/0 => -Infinity
0/0 => NaNAll these values are valid in the type number—but in my experience, they’re useless, so I don’t count them as valid return values. Some other languages don’t return such values. Instead, they throw an error:
(/ 1 0) ; throws ArithmeticError "Divide by zero"Division is a partial function due to one lousy value that breaks the type signature, whether the function throws an exception or returns a useless value.
Why are total functions important?
I think total functions are the next important concept from functional programming that needs to escape to the mainstream. Total functions make our code more reliable and easier to reason about. With a total function, we don’t need to worry about edge cases or unexpected behavior. Every input has a well-defined output, so we won’t accidentally send weird inputs as we build on them.
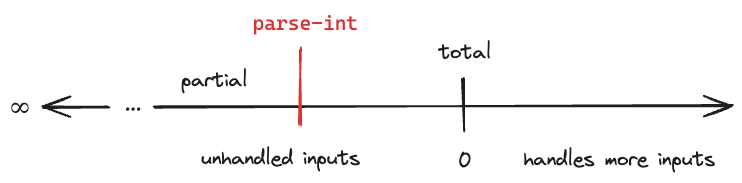
What if we saw the binary (partial/total) as a spectrum?
I often try to turn a binary into a spectrum. I did that for pure functions in Grokking Simplicity. To make an impure function pure, convert the implicit inputs to parameters and include the implicit outputs in the return value. Zero implicit inputs and outputs means it’s a pure function.
Just because you can’t get the implicit inputs and outputs to zero, it doesn’t mean reducing them isn’t beneficial. If your function reads from 3 global mutable variables and you reduce that to 2 or 1, your function is better off, even without all the benefits of it being pure.
The benefits of being pure are important. A pure function can be tested easily. It can be easily combined, moved, and erased by the compiler. These benefits are discontinuous since you only get them when you become fully pure. But we often forget that the other benefits, like how easy it is to reason about the function, are continuous. Getting rid of each implicit input makes your function easier to understand.
To make a partial function total, we must return a correct value for all valid parameter combinations. But making one more valid parameter return a valid output helps. So let’s consider it a continuous spectrum.
What lies beyond total functions?
Another question I ask is “What if I extend the trend?” Consider total function an interesting point on the line beyond which there are other interesting points. To the left of “total function”, there are various degrees of partiality, with more valid inputs causing errors. To the right, we could accept more “invalid” inputs (as long as we know how to handle them).
For example, let’s say we had a function called parse-int.
;; String -> Long (throws if can't parse)
(defn parse-int [s]
(Long/parseLong s))It’s partial. Not all strings can be parsed. We make it total by returning nil if there’s any trouble parsing:
;; String -> Long | nil
(defn parse-int [s]
(try
(Long/parseLong s)
(catch Exception e
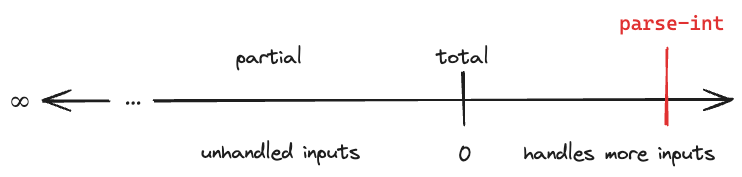
nil)))Great! It’s now total. But there’s more we can do. What about a string that’s almost parseable, like it has some whitespace at the beginning? Could we handle that? I can imagine software wanting that, so let’s pretend ours does and add it:
;; String -> Long | nil
(defn parse-int [s]
(try
(Long/parseLong (clojure.string/trim s))
(catch Exception e
nil)))We could handle more “invalid” inputs to this function. We could call it to-int instead of parse-int. It would convert a value to a long. What values could we convert to a long?
Strings
A Long itself (idempotent)
A Double
;; String | Long | Double -> Long | nil
(defn to-int [v]
(cond
(string? v)
(try
(Long/parseLong (clojure.string/trim s))
(catch Exception e
nil))
(int? v)
v
(double? v)
(long v)))We could go further with it.
As an example of a real function that does this, check out clojure.core/slurp. Here’s a list of the kinds of inputs it will take:
Reader
BufferedReader
InputStream
File
URI
If it’s a
file://URL, convert it to a File first
URL
Socket
byte arrays
character arrays
String
Try to parse it as a URL
Failing that, try to parse it as a local filename
I usually think this kind of function, which does a lot of magic to “do the right thing,” doesn’t have much place. I prefer to know the type I’ve got and call the right function to convert it to what I want. But sometimes I think they feel right—and this is one of those times. I’m trying to figure out when they feel right and when they don’t. In this case, I believe it feels right because the function:
reduces the system complexity by converging several different (potentially unknown) types down to one known type
remains a total function
Do you have ideas?
The other side of the coin: Avoiding invalid answers
I want to discuss the other side of the coin. In JavaScript, even with TypeScript’s protection, you still run into issues:
function divide(a: number, b: number): number {
return a/b;
}That could return a “real” number, or it could return NaN, Infinity, or -Infinity. Those last three values suck because they throw a monkey wrench in other arithmetic operations. They’re just waiting to cause trouble and this function will silently return them.
Let’s prevent that!
function divide(a: number, b: number): number {
if(b === 0) throw new Error("Divide by zero");
return a/b;
}Although this function is now partial, it does a better job at protecting our code from NaN and other pesky values. I think we do similar things in Clojure.
I see this behavior as the flip side of total functions. Total functions ask you to work for all valid inputs. This technique guarantees that a function will only return valid outputs. Do you have a name for this?
By the way, I think we need to use these in type-safe languages a lot as well, just perhaps not for the types of cases I’ve shown. For instance, there are values of numberOfMegabytes that will result in problems and you probably want to limit it:
function allocate(numberOfMegabytes: number): Array {
if(numberOfMegabytes > 1000) throw new Error("Can't allocate more than one gig");
...
}You could, of course, return undefined instead of throwing an error to keep it total.
Review and conclusion
I like the concept of total and partial functions. I hope that, just like pure/impure functions, it escapes the functional programming niche and enters the mainstream. I explored how we could turn the binary into a spectrum because a partial function being closer to total is better than not. But that opened up a world of possible inputs we could make valid past the special point on the spectrum called “total”. We saw what that could look like. I also brought up the idea that we often want to protect the return value. It’s a dual concern to the idea of total functions.
What techniques do you use to avoid functions returning bad values? How do you ensure that you only pass good values to your functions?
I speculated about why I thought that to-int was an okay function, even though it borders on “magical” type conversion. I think it has to do with its output being less complex than its input—and also being a total function. In the next issue, I want to expand on this idea, bring in “Postel’s Law”, complexity, and understandability.


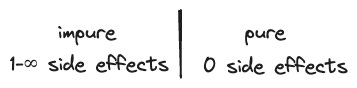





Could you wrap those partial functions in a Maybe?