Reversing the arrows
Is programming abstraction?
I published a new chapter of Runnable Specifications. It’s called Composition Lens Part 2. Please send me you comments and suggestions. I’m particularly interested in knowing what you find useful about it and anywhere you get stuck.
My talk from Heart of Clojure has been published. It’s called The Wonders of Abstraction. If you like this issue, you’ll like the talk.
Check out the line-up at Clojure/conj. Tickets are still available.
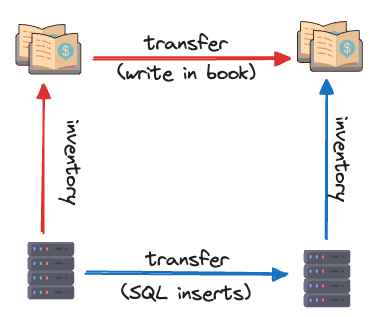
Two weeks ago, I wrote about writing bank software so that we could commute this diagram:
These two processes (moving gold and writing in ledgers) must both have mappings to and from the same abstraction. The operations in the double entry book involve writing numbers in books. The operations in the software involve INSERT statements in the database. They are both concrete systems that operate in the physical world.
But recently I’ve been turning this over and thinking of the medium as an abstract domain. Let me explain by way of Euclid.
In Euclidean geometry, we use three instruments, a pencil, a straight edge, and a compass. Using these tools help us understand how the abstract concepts of lines, points, angles, etc., actually operate. It’s an odd relationship. We draw concrete pictures to tell us about the abstract domain. Raphael captured the sublime feeling of a geometric proof coming together:
Notice that the man in the center is pointing down to the chalkboard while looking up to the heavens. There’s something mysterious going on where we learn about all lines by drawing a particular line.
Despite the mystery, something is very clear: By paring down the available operations to a small formal set (drawing points, drawing lines, drawing arcs, etc.; in other words, there are no squiggles), we’re able to discover truths universal to that formal set of operations. And the things we learn are useful in engineering, architecture, and other fields dealing with space.
Similarly, we can see the ledger as a kind of small formal set of operations. Each entry in the ledger has a meaning (a debit or credit) within the system. We can describe universal features of all ledgers, while only having encountered a small number of them. Is the ledger just an instrument to help our mind keep track of the abstract accounts?
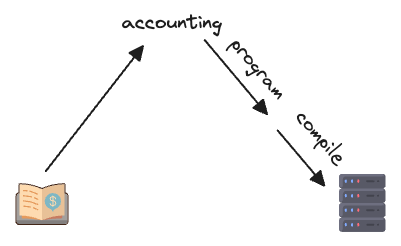
I’m not trying to bring up philosophical puzzles between materialism and idealism. Instead, I’ve been playing with the idea that computer programming can be both an upward arrow and a downward arrow.
That is, we can think of programming as an implementation of an abstract idea that runs on a computer.
Or we can think of programming as developing a mapping from a concrete domain into an abstract realm defined by computation.
And this has the same structure as Euclidean geometry, but this time the instrument is the computer. We’re using a concrete machine to talk about abstract, universal truths.
It seems far fetched. But Turing showed something really important: It doesn’t matter what your computer is made of. As long as the computers are “complete”, they’re all equivalent. That is, they’re all concrete instances of an abstract idea of computation.
Likewise, the machine code of any particular computer is a small, formal system of abstract operations. The programming language we write in is also a formal, abstract system that maps to that abstract machine code. And then we write definitions of banking concepts in that programming language. All of these are mappings that lose information, and so they are all abstractions.
Now, let me be very clear: There are two possible perspectives, and they’re both valid. The first, common one is that programming is the act of taking our abstract ideas and making them concrete by, eventually, commanding a microchip to switch the right parts of it from high to low voltage and vice versa so that it gets the right result. It’s a downward arrow, getting more and more concrete as we go.
The second, less common one is that programming is the act of taking a abstract ideas and mapping it to an even more abstract domain of ones and zeros. And then to make it work, we load it into a concrete computer and run it.
I’ve worked under the first perspective most of my life. But I’m finding a lot of fruit in taking on the second one. I’ll talk a bit about what I’m finding in the next issue. But before then, I’d love to know your thoughts on this. What do you think about these two perspectives?








The point of your post seems to be that abstraction is a process with its own value. Which is why engineering, if it is understood as "implementing a pre-existing abstract idea", misses an important point. Yet that insight should not be muddled with the Platonic image of the abstract stuff being somewhere "above", like the man in Raphael's painting. Abstractions are important insofar they manage to be effective in practice, and this practice, in turn, influences the abstractions we can (and should) use. That's an interactive relation, not one where we end up having "the truth" on one side. Abstractions are tools, and their ability to contribute to what we do (most often, thinking) is why they are so important and so valuable.
Anyways, I like this perspective on what programmers do.